Catching Up & Happy Birthday

Catching Up & Happy Birthday#

First of all, let me say I’m sorry for missing last week’s tutorial. There is no excuse:

*Luna Kepler was born on January 18th, 2024, and was the cause of ML for Neuroscientists' tutor to be absent from class. Fatherly*

Exploratory Data Analysis (EDA)#

Our main goal while doing EDA is to summarize main characteristics of our dataset.

It’s crucial that we understand what our data is composed of.

First, we take a look.#

"""
configuration.py

Constants defined for data retrieval and preprocessing.
"""

# GitHub data directory URL.
DATA_DIRECTORY = (
    "https://raw.githubusercontent.com/mdcollab/covidclinicaldata/master/data/"
)

# Pattern for composing CSV file URLS to read.
CSV_FILE_PATTERN = "{week_id}_carbonhealth_and_braidhealth.csv"
CSV_URL_PATTERN = f"{DATA_DIRECTORY}/{CSV_FILE_PATTERN}"

# *week_id*s used to format CSV_FILE_PATTERN with.
WEEK_IDS = (
    "04-07",
    "04-14",
    "04-21",
    "04-28",
    "05-05",
    "05-12",
    "05-19",
    "05-26",
    "06-02",
    "06-09",
    "06-16",
    "06-23",
    "06-30",
    "07-07",
    "07-14",
    "07-21",
    "07-28",
    "08-04",
    "08-11",
    "08-18",
    "08-25",
    "09-01",
    "09-08",
    "09-15",
    "09-22",
    "09-29",
    "10-06",
    "10-13",
    "10-20",
)

# Values replacement dictionary by column name.
REPLACE_DICT = {"covid19_test_results": {"Positive": True, "Negative": False}}

# Name of the column containing the COVID-19 test results.
TARGET_COLUMN_NAME = "covid19_test_results"

# Fractional threshold of missing values in a feature.
NAN_FRACTION_THRESHOLD = 0.5

# Prefix used in columns containing X-ray data results.
X_RAY_COLUMN_PREFIX = "cxr_"

	test_name	swab_type	covid19_test_results	age	high_risk_exposure_occupation	high_risk_interactions	diabetes	chd	htn	cancer	asthma	copd	autoimmune_dis	smoker	temperature	pulse	sys	dia	rr	sats	rapid_flu_results	rapid_strep_results	ctab	labored_respiration	rhonchi	wheezes	days_since_symptom_onset	cough	cough_severity	fever	sob	sob_severity	diarrhea	fatigue	headache	loss_of_smell	loss_of_taste	runny_nose	muscle_sore	sore_throat	er_referral
0	SARS COV 2 RNA RTPCR	Nasopharyngeal	False	58	True	nan	False	False	False	False	False	False	False	False	36.950000	81.000000	126.000000	82.000000	18.000000	97.000000	nan	nan	False	False	False	False	28.000000	True	Severe	nan	False	nan	False	False	False	False	False	False	False	False	False
1	SARS-CoV-2, NAA	Oropharyngeal	False	35	False	nan	False	False	False	False	False	False	False	False	36.750000	77.000000	131.000000	86.000000	16.000000	98.000000	nan	nan	False	False	False	False	nan	True	Mild	False	False	nan	False	False	False	False	False	False	False	False	False
2	SARS CoV w/CoV 2 RNA	Oropharyngeal	False	12	nan	nan	False	False	False	False	False	False	False	False	36.950000	74.000000	122.000000	73.000000	17.000000	98.000000	nan	nan	nan	nan	nan	nan	nan	False	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	False
23498	SARS-CoV-2, NAA	Nasal	False	35	False	False	False	False	False	False	False	False	False	False	37.000000	69.000000	136.000000	84.000000	12.000000	100.000000	nan	nan	False	nan	nan	nan	nan	False	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
23499	SARS-CoV-2, NAA	Nasal	False	24	False	True	False	False	False	False	False	False	False	False	36.750000	70.000000	128.000000	78.000000	12.000000	99.000000	nan	nan	nan	False	False	False	nan	False	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
23500	SARS-CoV-2, NAA	Nasal	False	52	False	False	False	False	False	False	False	False	False	False	37.000000	94.000000	165.000000	82.000000	12.000000	98.000000	nan	nan	nan	False	False	False	7.000000	True	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
46996	SARS-CoV-2, NAA	Nasal	False	11	False	False	False	False	False	False	False	False	False	False	36.900000	78.000000	116.000000	79.000000	16.000000	100.000000	nan	nan	True	False	True	True	nan	False	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
46997	SARS-CoV-2, NAA	Nasal	False	30	False	False	False	False	False	False	False	False	False	False	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	False	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
46998	SARS-CoV-2, NAA	Nasal	False	36	False	False	False	False	False	False	False	False	False	False	36.850000	81.000000	122.000000	81.000000	14.000000	100.000000	nan	nan	nan	False	nan	nan	7.000000	True	Mild	False	True	Mild	True	True	True	False	False	False	True	False	nan
70494	Rapid COVID-19 PCR Test	Nasal	False	32	False	nan	False	False	False	False	False	False	False	False	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	False	nan	nan	False	nan	False	False	False	False	False	False	False	False	nan
70495	SARS-CoV-2, NAA	Nasal	False	59	False	False	False	False	True	False	False	False	False	False	36.600000	75.000000	137.000000	99.000000	nan	97.000000	nan	nan	False	False	False	False	7.000000	True	Moderate	True	False	nan	False	False	False	False	False	False	False	True	nan
70496	SARS-CoV-2, NAA	Nasal	False	27	False	True	False	False	False	False	False	False	False	False	37.000000	63.000000	113.000000	71.000000	15.000000	98.000000	nan	nan	nan	False	nan	nan	2.000000	False	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
93992	SARS-CoV-2, NAA	Nasal	False	33	False	nan	False	False	False	False	False	False	False	False	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	False	nan	nan	False	nan	False	False	False	False	False	False	False	False	nan
93993	Rapid COVID-19 PCR Test	Nasal	False	46	False	False	False	False	False	False	False	False	False	False	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	False	nan	False	False	nan	False	False	False	False	False	False	False	False	nan
93994	Rapid COVID-19 PCR Test	Nasal	False	53	False	nan	False	False	True	False	False	False	False	False	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	nan	False	nan	nan	False	nan	False	False	False	False	False	False	False	False	nan

Alright! Some things that we can already learn about our dataset from this table are:

It contains a total of 93995 observations.
There are 41 columns with mixed data types (numeric and categorical).
Missing values certainly exist (we can easily spot nan entries).
The subsample raises a strong suspicion that dataset is imbalanced, i.e. when examining our target variable (‘covid19_test_results’) it seems there are far more negative observations than positive ones. A quick sum() call reveals that indeed only 1313 of the 93995 observations are positive.

Missing Values

Handling missing values requires careful judgement. Possible solutions include:

Removing the entire feature (column) containing the missing values.
Removing all observations with missing values.
Imputation: “Filling in” missing values with some constant or statistic, such as the mean or the mode.

The approach we’ll take when dealing with missing values depends heavily on the structure of our data, for example:

If a column contains a small number of observations (relative to the size of the dataset) and the dataset is rich enough and offers more features that could be expected to be informative, it might be best to remove it.
If the dataset is large and the feature in question is crucial for the purposes of our analysis, remove all observations with missing values.
Imputation might sound like a good trade-off if there is a good reason to believe some statistic may adequately approximate the missing values, but it is also the subject of many misconceptions and often used poorly.
There are also ML methods that can safely include missing values (such as decision trees). We will learn when and how these are used later in this course.

data = clean_missing_values(data)

Once the dataset is clean of any missing values, we can go on to inspect the kind of features that are available for us.

X = data.drop(TARGET_COLUMN_NAME, axis=1)

categorial_features = X.select_dtypes(["object", "bool"])
numerical_featuers = X.select_dtypes(exclude=["object", "bool"])

print("Categorial features:\n" + ", ".join(categorial_features.columns))
print("\nNumerical features:\n" + ", ".join(numerical_featuers.columns))

Categorial features:
test_name, swab_type, high_risk_exposure_occupation, high_risk_interactions, diabetes, chd, htn, cancer, asthma, copd, autoimmune_dis, smoker, labored_respiration, cough, fever, sob, diarrhea, fatigue, headache, loss_of_smell, loss_of_taste, runny_nose, muscle_sore, sore_throat

Numerical features:
age, temperature, pulse, sats

We are left with 28 features and 37754 observations (718 of which are positive).

Visualization#

Simply looking at the values in our data isn’t enough. It’s helpful to visualize how different variables interact with each out, how the distribute, etc.

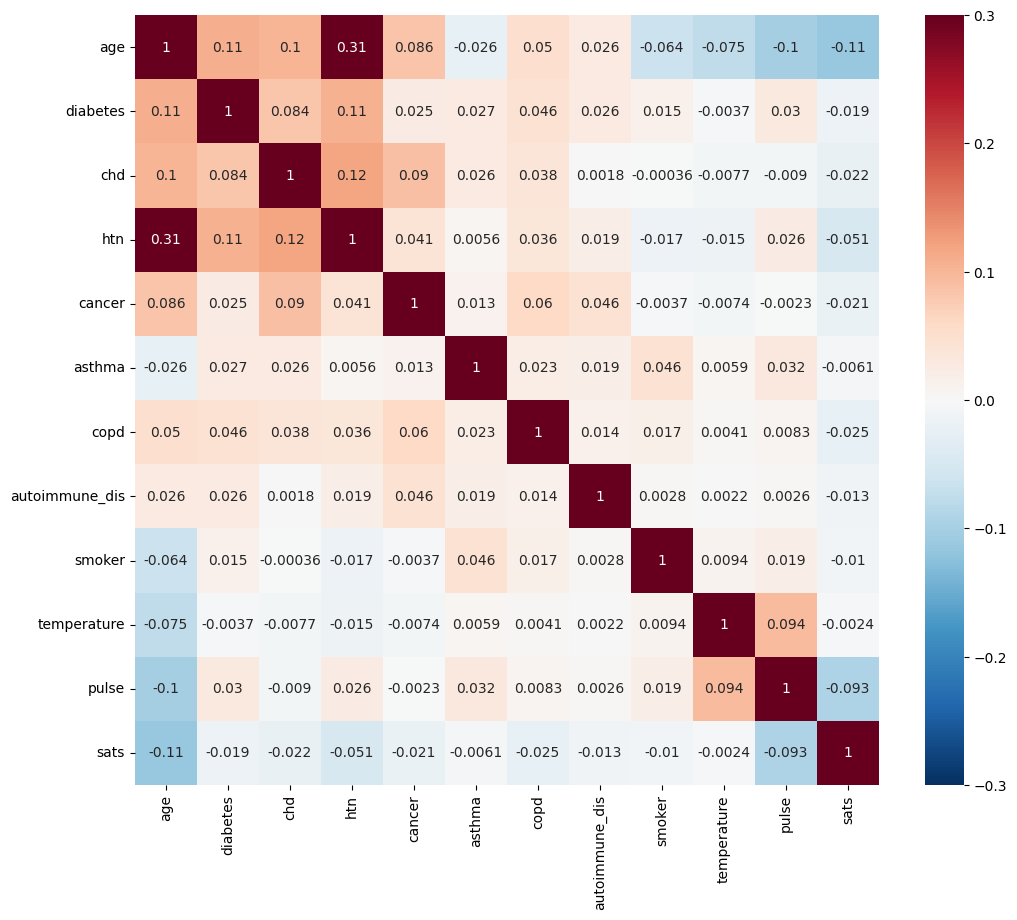
Feature Correlations#

import matplotlib.pyplot as plt
import seaborn as sns

correlation_matrix = X.corr(numeric_only=True)
fig, ax = plt.subplots(figsize=(12, 10))
_ = sns.heatmap(correlation_matrix, annot=True,vmin=-.3, vmax=.3, center=0, cmap="RdBu_r", ax=ax)

../../_images/5202a681f74efc18f4d336a98eec3a05dc4056a709f6203e51698b486b627021.png

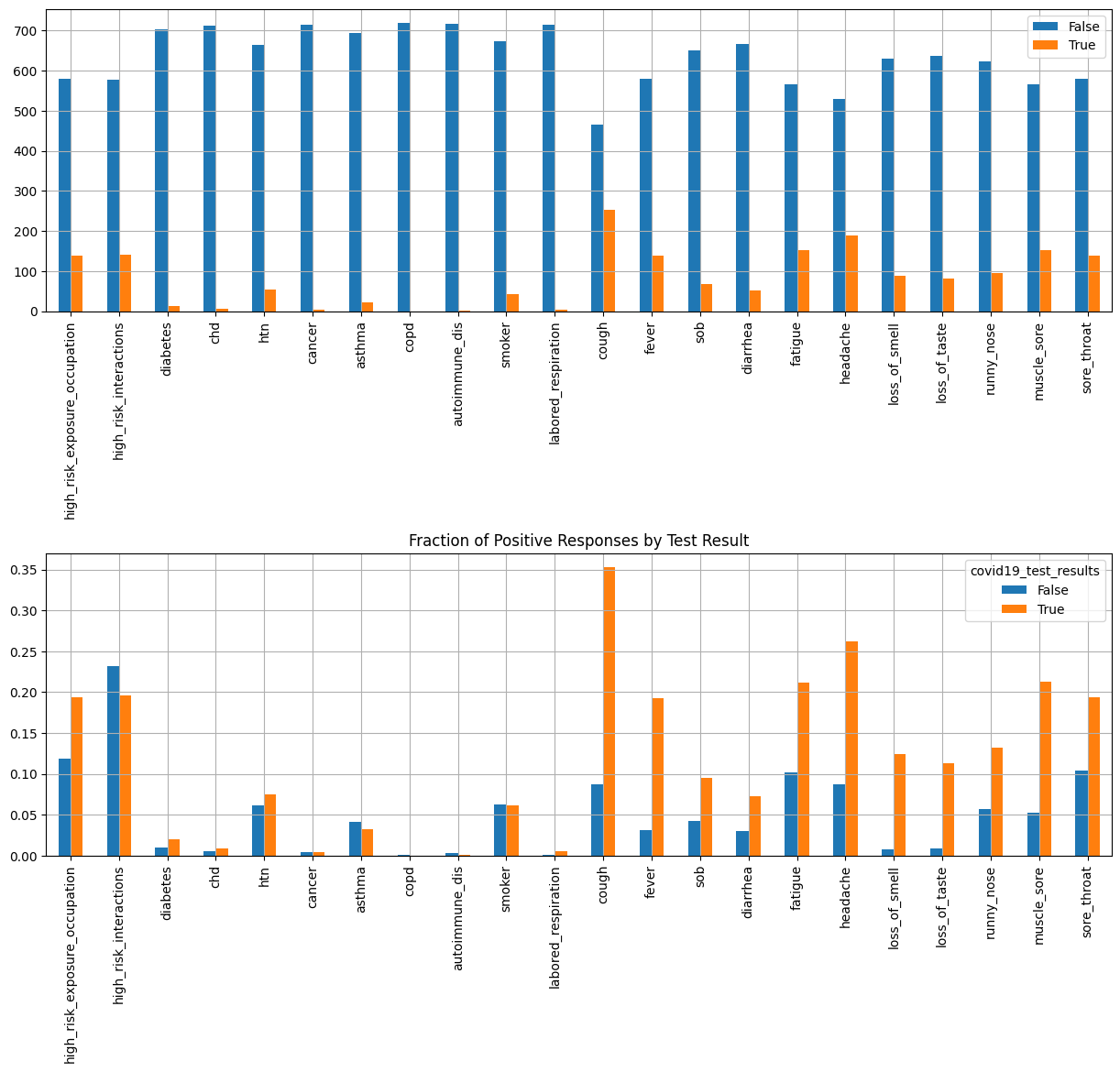
Categorial Features#

import pandas as pd
plt.rcParams['axes.grid'] = True

boolean_features = X.select_dtypes(["bool"])
positives = boolean_features[target]
value_counts = {}
for column in positives:
    value_counts[column] = positives[column].value_counts()
value_counts = pd.DataFrame(value_counts)

fig, axes = plt.subplots(2,1,figsize=(15, 12))
_ = value_counts.T.plot(kind="bar", ax=axes[0])
_ = plt.title("Symptoms in Positive Patients")
_ = ax.set_xlabel("Feature")
_ = ax.set_ylabel("Count")
plt.grid()

# Group all boolean features by the target variable (COVID-19 test result)
grouped = boolean_features.groupby(target)

# Calculate the fraction of positives in each group.
fractions = grouped.sum() / grouped.count()

_ = fractions.T.plot(kind="bar", ax=axes[1])
_ = plt.title("Fraction of Positive Responses by Test Result")
_ = ax.set_xlabel("Feature")
_ = ax.set_ylabel("Fraction")

plt.subplots_adjust(hspace=0.8)

../../_images/850d9ab7458b2a570d441208c59d274ddaa1b7c32fdea6d76f056db823e36e1b.png

Numerical Features#

# Select all numerical features.
numerical_features = X.select_dtypes(["float64", "int64"])

# Create distribution plots.
nrows = len(numerical_features.columns)
fig, ax = plt.subplots(nrows=nrows, ncols=2, figsize=(15, 30))
for i, feature in enumerate(numerical_features):
    sns.violinplot(x=TARGET_COLUMN_NAME, y=feature, hue=TARGET_COLUMN_NAME, data=data, ax=ax[i, 0], legend=False)
    if i == 0:
        ax[i, 0].set_title("Violin Plots")
        ax[i, 1].set_title("Box Plots")        
    sns.boxplot(x=TARGET_COLUMN_NAME, y=feature, hue=TARGET_COLUMN_NAME, data=data, ax=ax[i, 1], legend=False)
    ax[i, 0].set_xlabel("")
    ax[i, 1].set_xlabel("")
    ax[i, 1].set_ylabel("")
_ = fig.text(0.5, 0, "COVID-19 Test Results", ha='center')
_ = fig.suptitle("Numerical Feature Distributions", y=1)
fig.tight_layout()

../../_images/b4858c6977b204c9a9ce03120f2d36d282e5449af899d78e32eea8c137ee0024.png

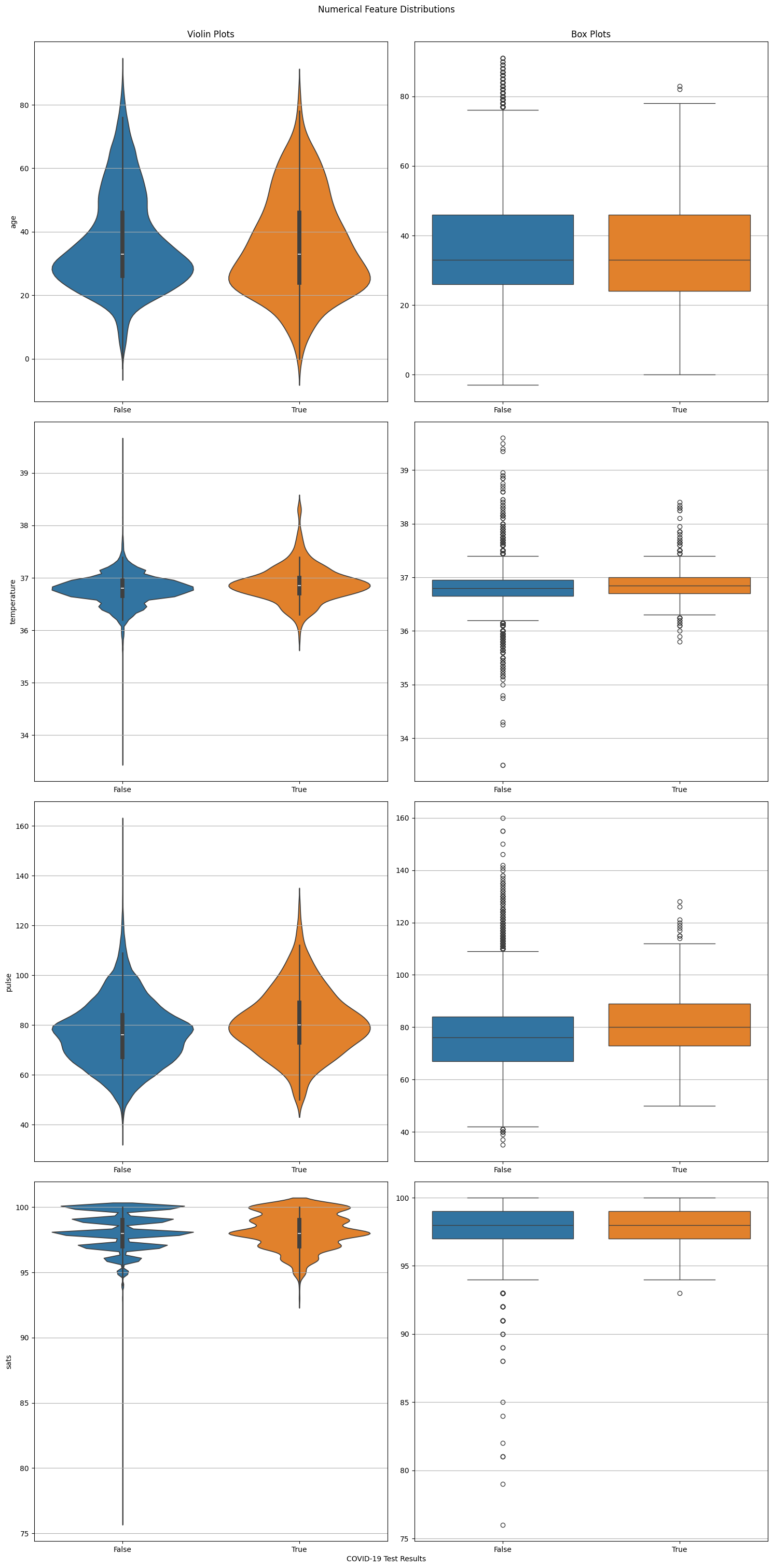
Note

Violin plots are essentially box plots combined with a kernel density estimation. While box plots give us a good understanding of the data’s quartiles and outliers, violin plots provide us with an informative representation of it’s entire distribution.

k-Nearest Neighbors (k-NN)#

k-NN is a simple and useful non-parametric method that is commonly used for both classification and regression. It relies on having some method of calculating distance between data points, and using the the “nearest” observations to predict the target value for new ones.

KNN Illustration — Example of k-NN classification. The test sample (green dot) should be classified either to blue squares or to red triangles. If k = 3 (solid line circle) it is assigned to the red triangles because there are 2 triangles and only 1 square inside the inner circle. If k = 5 (dashed line circle) it is assigned to the blue squares (3 squares vs. 2 triangles inside the outer circle). Wikipedia

Loading the Dataset#

Basic Exploration#

import numpy as np

# Class colors
COLORS = "rgba(255, 0, 0, 0.3)", "rgba(0, 255, 0, 0.3)", "rgba(0, 0, 255, 0.3)"

# Create a unified dataframe.
data = pd.concat([X, y], axis="columns")


# Set class background color
def set_class_color(class_index: str) -> str:
    return f"background-color: {COLORS[class_index]};"


def set_class_name(class_index: str) -> str:
    return iris_dataset.target_names[class_index]


# Select some sample indices
sample_indices = np.linspace(0, len(data) - 5, 3, dtype=int)
sample_indices = [index for i in sample_indices for index in range(i, i + 5)]

# Display table
data.iloc[sample_indices, :].style.background_gradient().map(lambda x: set_class_color(x), subset=[TARGET_NAME]).format(
    {TARGET_NAME: set_class_name}).set_properties(**{
        "border": "1px solid black"
    }, subset=[TARGET_NAME]).set_properties(**{
        "text-align": "center"
    }).set_table_styles([
        dict(selector="th", props=[("font-size", "14px")]),
        dict(selector="td", props=[("font-size", "12px")]),
    ]).format("{:.2f}", subset=[col for col in data.columns if col != TARGET_NAME])

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	class
0	5.10	3.50	1.40	0.20	setosa
1	4.90	3.00	1.40	0.20	setosa
2	4.70	3.20	1.30	0.20	setosa
3	4.60	3.10	1.50	0.20	setosa
4	5.00	3.60	1.40	0.20	setosa
72	6.30	2.50	4.90	1.50	versicolor
73	6.10	2.80	4.70	1.20	versicolor
74	6.40	2.90	4.30	1.30	versicolor
75	6.60	3.00	4.40	1.40	versicolor
76	6.80	2.80	4.80	1.40	versicolor
145	6.70	3.00	5.20	2.30	virginica
146	6.30	2.50	5.00	1.90	virginica
147	6.50	3.00	5.20	2.00	virginica
148	6.20	3.40	5.40	2.30	virginica
149	5.90	3.00	5.10	1.80	virginica

Train/Test Split#

Train-Test Split

A lot can be said regarding the different approaches for model validation and evaluation (which we’ll discuss later in the course), but the general guideline is that, since our model should detect underlying trends in the data, we would evaluate its performance over unseen data. Therefore, we’ll split our data into a training (for model fitting) and testing (for evaluation).

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    random_state=0,
                                                    test_size=0.25)

We now have a training dataset consisting of 112 observations and a test dataset with 38 observations.

Model Creation#

Models and Estimators

Machine Learning algorithms and models are easily accesible through numberous packages, namely scikit-learn. While different estimators provide different advantages and pitfalls, they share some basic properties, making it easy for users to use them.

*Since these estimators are basically just algorithms and formulas that need to be tailored to the dataset being used, all estimators have a ‘fit’ method, (unsurprisingly) fitting the estimators to generalize to any specific data.

from sklearn.neighbors import KNeighborsClassifier

k = 1

knn = KNeighborsClassifier(n_neighbors=k)
_ = knn.fit(X_train, y_train)

Model Evaluation#

Misclassification Rate / Accuracy#

import numpy as np

y_predicted = knn.predict(X_test)

misclassification_rate = np.mean(y_predicted != y_test) * 100

Our model achieved a misclassification_rate of ‘2.632’%, meaning it correctly predicted np.int64(37) of 38 target values in our test set.

Another way to look at it is:

from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_predicted) * 100

97.36842105263158

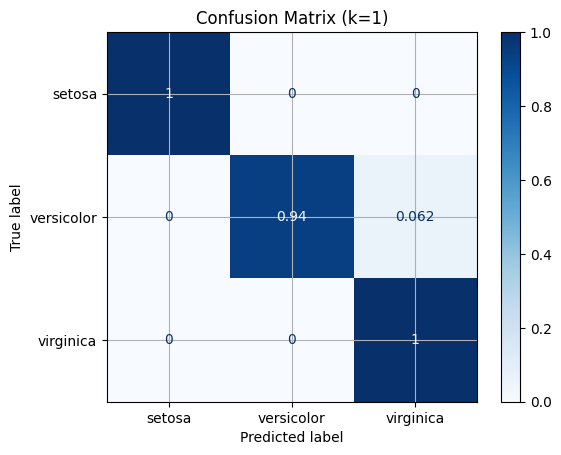
Confusion Matrix#

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_predicted)

array([[13,  0,  0],
       [ 0, 15,  1],
       [ 0,  0,  9]])

import matplotlib.pyplot as plt

from sklearn.metrics import ConfusionMatrixDisplay


disp = ConfusionMatrixDisplay.from_estimator(knn,
                             X_test,
                             y_test,
                             display_labels=iris_dataset.target_names,
                             cmap=plt.cm.Blues,
                             normalize="true")
_ = disp.ax_.set_title(f"Confusion Matrix (k={k})")

../../_images/4b954a876353b6dfc64329e34c44a6c4ac3a9978f87e859034cca695444b94f8.png

Linear Regression#

In statistics, linear regression is a linear approach to modeling the relationship between a scalar response (or dependent variable) and one or more explanatory variables (or independent variables). Wikipedia

Using linear regression with Python is as easy as running:

>>> from sklearn.linear_model import LinearRegression
>>> model = LinearRegression()
>>> model.fit(X_train, y_train)
>>> predictions = model.predict(X_test)

First, let’s reproduce scikit-learn’s Linear Regerssion Example using the prepackaged diabetes dataset.

Loading the dataset#

import pandas as pd

from sklearn import datasets

# Read the dataset as a pandas DataFrame
dataset = datasets.load_diabetes(as_frame=True)

# Create observations matrix and target vector
X, y = dataset.data, dataset.target

# Create a unified DataFrame containing both
data = pd.concat([X, y], axis=1)

Raw Inspection#

import numpy as np
import pandas as pd

# Select some sample indices
sample_indices = np.linspace(0, len(X) - 4, 4, dtype=int)
sample_indices = [index for i in sample_indices for index in range(i, i + 4)]

# Print data table (features and target)
data.iloc[sample_indices, :].style.set_properties(**{
    "text-align": "center",
}).set_properties(**{
    "border-left": "4px solid black"
}, subset=['target']).set_table_styles([
    dict(selector="th", props=[("font-size", "13px")]),
    dict(selector="td", props=[("font-size", "11px")]),
]).background_gradient().format("{:.3f}")

	age	sex	bmi	bp	s1	s2	s3	s4	s5	s6	target
0	0.038	0.051	0.062	0.022	-0.044	-0.035	-0.043	-0.003	0.020	-0.018	151.000
1	-0.002	-0.045	-0.051	-0.026	-0.008	-0.019	0.074	-0.039	-0.068	-0.092	75.000
2	0.085	0.051	0.044	-0.006	-0.046	-0.034	-0.032	-0.003	0.003	-0.026	141.000
3	-0.089	-0.045	-0.012	-0.037	0.012	0.025	-0.036	0.034	0.023	-0.009	206.000
146	-0.031	0.051	0.060	0.001	0.012	0.032	-0.043	0.034	0.015	0.007	178.000
147	-0.056	-0.045	0.093	-0.019	0.015	0.023	-0.029	0.025	0.026	0.040	128.000
148	-0.060	0.051	0.015	-0.019	0.037	0.048	0.019	-0.003	-0.031	-0.001	96.000
149	-0.049	0.051	-0.005	-0.047	-0.021	-0.020	-0.069	0.071	0.061	-0.038	126.000
292	0.009	-0.045	-0.022	-0.032	-0.050	-0.069	0.078	-0.071	-0.063	-0.038	84.000
293	-0.071	-0.045	0.093	0.013	0.020	0.043	0.001	0.000	-0.055	-0.001	200.000
294	0.024	0.051	-0.031	-0.006	-0.017	0.018	-0.032	-0.003	-0.074	-0.034	55.000
295	-0.053	0.051	0.039	-0.040	-0.006	-0.013	0.012	-0.039	0.016	0.003	85.000
438	-0.006	0.051	-0.016	-0.068	0.049	0.079	-0.029	0.034	-0.018	0.044	104.000
439	0.042	0.051	-0.016	0.017	-0.037	-0.014	-0.025	-0.011	-0.047	0.015	132.000
440	-0.045	-0.045	0.039	0.001	0.016	0.015	-0.029	0.027	0.045	-0.026	220.000
441	-0.045	-0.045	-0.073	-0.081	0.084	0.028	0.174	-0.039	-0.004	0.003	57.000

Feature Correlation#

We can use seaborn’s heatmap function to inspect feature correlations.

import seaborn as sns

# Calculate correlation matrix using NumPy
correlation_matrix = np.corrcoef(data.values.T)

# Plot correlation matrix using seaborn
fig, ax = plt.subplots(figsize=(8, 8))
tick_labels = list(X.columns) + ['diabetes']
hm = sns.heatmap(
    correlation_matrix,
    ax=ax,
    cbar=True,  # Show colorbar
    cmap="vlag",  # Specify colormap
    vmin=-1,  # Min. value for colormapping
    vmax=1,  # Max. value for colormapping
    annot=True,  # Show the value of each cell
    square=True,  # Square aspect ratio in cell sizing
    fmt='.2f',  # Float formatting
    annot_kws={'size':
               12},  # Font size of the values displayed within the cells
    xticklabels=tick_labels,  # x-axis labels
    yticklabels=tick_labels)  # y-axis labels
plt.tight_layout()
plt.show()

../../_images/1cb9838b894d1240331cdf439a0a323bc90a8b178a5de401e393c452c010ef54.png

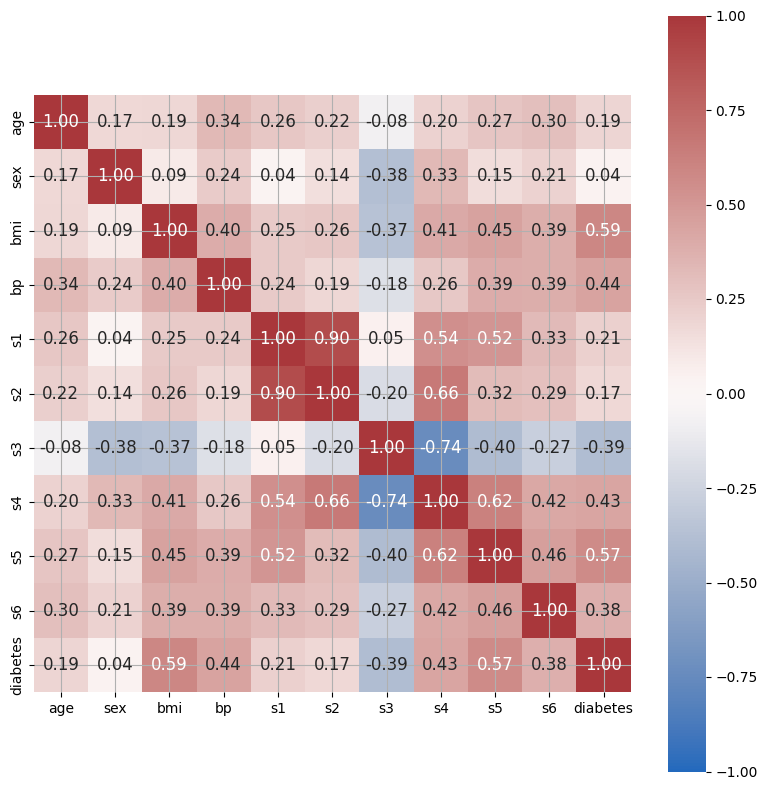
Simple Linear Regression#

Simple linear regression is a linear regression model with a single explanatory variable. bmi seems to show a discernible linear relationship with the target variable, so let’s go with that one.

from sklearn.model_selection import train_test_split

# Create a vector of the single predictor values
simple_X = X.bmi.to_numpy().reshape(len(X), 1)

# Split for simple linear regression
simple_X_train, simple_X_test, y_train, y_test = train_test_split(simple_X,
                                                                  y,
                                                                  random_state=0,
                                                                  test_size=0.2)

Model Creation#

from sklearn.linear_model import LinearRegression

model = LinearRegression()
_ = model.fit(simple_X_train, y_train)

Model Application#

simple_y_pred = model.predict(simple_X_test)

Model Evaluation#

First, we’ll plot our predicted values alongside the observed values, as well as the regression line estimated by our model.

# Create figure
fig, ax = plt.subplots(figsize=(15, 7))

# Plot real values scatter plot
_ = plt.scatter(simple_X_test, y_test, color="black", label="Real Values")

# Plot predicted values scatter plot
_ = plt.scatter(simple_X_test,
                simple_y_pred,
                color="red",
                label="Predicted Values")

# Plot regression line
_ = plt.plot(simple_X_test,
             simple_y_pred,
             color="blue",
             label="Regression Line")

# Show legend
_ = plt.legend()

# Set title
title = "Disease Progression by BMI"
plt.title(title)

# Sex axis labels
ax.set_xlabel("Standardized BMI score")
_ = ax.set_ylabel("Disease Progression")

../../_images/06d4e436c135c436e2793656dd392ca7b097dbae236029f2657e2d7ee654e5f7.png

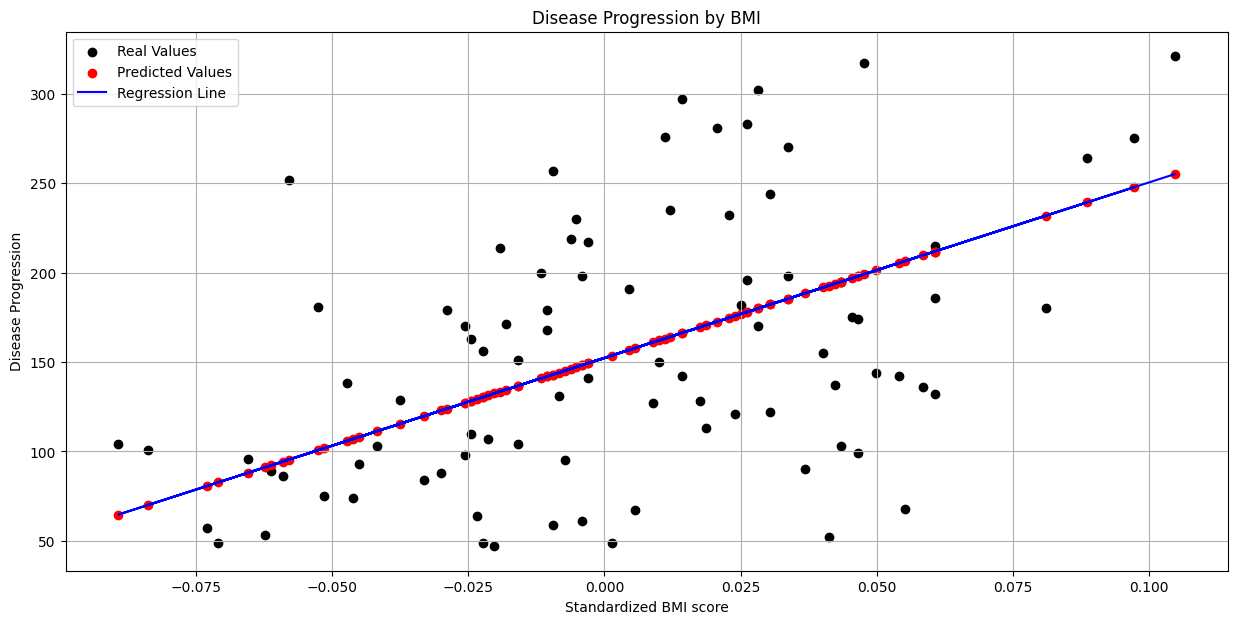
We can also use the sklearn.metrics module to calculate the MSE and coefficient of determination ($R^2$).

from sklearn.metrics import mean_squared_error, r2_score

mse = mean_squared_error(y_test, simple_y_pred)
r_squared = r2_score(y_train, model.predict(simple_X_train))
print(f"Coefficient: {model.coef_[0]:.2f}")
print(f"Intercept: {model.intercept_:.2f}")
print(f'Mean Squared Error: {mse:.2f}')
print(f'Coefficient of Determination: {r_squared:.2f}')

Coefficient: 981.66
Intercept: 152.29
Mean Squared Error: 4150.68
Coefficient of Determination: 0.38

Multiple Linear Regression#

General notation:

$OLS$

Calculating the coefficient vector of the least-squares hyperplane:

$OLS beta hat$

Multiple Linear Regression using `sklearn`#

Model Creation#

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    random_state=0,
                                                    test_size=0.2)

multiple_model = LinearRegression()
_ = multiple_model.fit(X_train, y_train)

Model Application#

y_pred_all = multiple_model.predict(X_test)

Model Evaluation#

mse_all = mean_squared_error(y_train, multiple_model.predict(X_train))
r2_score_all = r2_score(y_train, multiple_model.predict(X_train))

betas_all = [beta.round(2) for beta in multiple_model.coef_.flatten()]

print(f"Coefficient: {betas_all}")
print(f'Mean Squared Error: {mse_all:.2f}')
print(f'Coefficient of Determination: {r2_score_all:.2f}')

Coefficient: [np.float64(-35.55), np.float64(-243.17), np.float64(562.76), np.float64(305.46), np.float64(-662.7), np.float64(324.21), np.float64(24.75), np.float64(170.32), np.float64(731.64), np.float64(43.03)]
Mean Squared Error: 2734.75
Coefficient of Determination: 0.55

Catching Up & Happy Birthday

Contents

Catching Up & Happy Birthday#

Exploratory Data Analysis (EDA)#

First, we take a look.#

Visualization#

Feature Correlations#

Categorial Features#

Numerical Features#

k-Nearest Neighbors (k-NN)#

Loading the Dataset#

Basic Exploration#

Train/Test Split#

Model Creation#

Model Evaluation#

Misclassification Rate / Accuracy#

Confusion Matrix#

Linear Regression#

Loading the dataset#

Raw Inspection#

Feature Correlation#

Simple Linear Regression#

Model Creation#

Model Application#

Model Evaluation#

Multiple Linear Regression#

Multiple Linear Regression using sklearn#

Model Creation#

Model Application#

Model Evaluation#

Multiple Linear Regression using `sklearn`#